L’analisi dei segnali climatici: le wavelets (I Parte)

Cap. Franco Colombo

Premessa

La maggior parte dei segnali naturali non sono stazionari e contengono componenti transitorie che eccitano un ampio intervallo di frequenze in un piccolo intervallo di tempo. Sembra che la classica analisi di Fourier non sia adeguata per il trattamento di questi segnali, dato che tutte le informazioni sulla localizzazione temporale di una data frequenza vengono perse nel processo analitico. Questo portò innanzitutto all’analisi spettrale con finestre mobili (Berger et al., 1990; Yiou et al., 1991; Birchfield e Ghil, 1993) e successivamente a rappresentazioni tempo-frequenza più elaborate, cioè, le trasformate wavelet.

Le analisi wavelet furono utilizzate per la prima volta in modo indipendente nella fisica da A. Grossmann, in geofisica da Morlet e in matematica da Y. Meyer. La loro popolarità nel campo dell’elaborazione dei dati è dovuta in gran parte al lavoro di S. Mallat sulla analisi di immagini digitali (Mallat, 1989). Sono state utilizzate nell’analisi della turbolenza bi-dimensionale (Farge e Rabreau, 1988), nella meteorologia (Gao e Li, 1993; Meyers et al., 1993) e nella paleoclimatologia (Bolton et al., 1995; Yiou et al., 1996). Le applicazioni delle trasformate wavelet sono state esaminate in modo approfondito da Grossmann et al. (1989) e Farge (1992). Le basi matematiche si trovano in Meyer (1989).

Scopo della prima parte di questo articolo vuole essere quello di illustrare, seppur nelle sue linee essenziali, il metodo di analisi wavelet e la sua evoluzione nel tempo. Nella seconda parte dell’articolo, attualmente in fase di elaborazione, si descriveranno le applicazioni possibili su una serie temporale di dati meteorologici.

Introduzione

Per capire l’origine di qualsiasi segnale naturale è necessario analizzarlo. Così i tremori sismici, la voce umana, le vibrazioni di un motore, le immagini mediche, i dati finanziari, la musica, la temperatura e molti altri tipi di segnali naturali, hanno molto spesso bisogno di essere efficientemente codificati, compressi, ripuliti, ricostruiti, descritti, semplificati, modellati, distinti o localizzati. Le wavelet rappresentano un nuovo e promettente set di strumenti di analisi che permette di fare tutto ciò.

L’analisi di Fourier

Per poter analizzare un qualsiasi segnale naturale, esistono un’enorme quantità di strumenti matematici e tecniche di analisi.

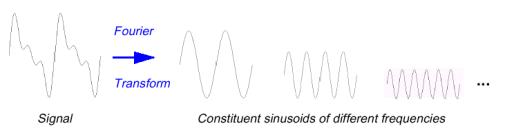
La più conosciuta ed utilizzata e sicuramente l’analisi di Fourier, la quale decompone il segnale in costituenti sinusoidali di differenti frequenze. Essa consente quindi di vedere il nostro segnale non più nel dominio del tempo ma nel dominio delle frequenze.

Quando è molto importante la ricerca del contenuto in frequenza di un segnale,l’analisi di Fourier risulta estremamente utile.

Tuttavia essa presenta una grave inconveniente: durante la trasformazione nel dominio della frequenza, l’informazione nel dominio del tempo viene completamente persa. Quando osserviamo la trasformata di Fourier di un segnale, è impossibile dire quando un particolare evento si sia verificato.

Se un segnale non cambia molto nel tempo, ovvero se stiamo analizzando un segnale cosiddetto “stazionario”, tale inconveniente non è molto importante.

La gran parte dei segnali fisici, in modo particolare quelli meteorologici, contengono numerose caratteristiche “non stazionarie” o transitorie: derive, trend, repentini cambiamenti etc.. Queste caratteristiche rappresentano spesso la parte più importante del segnale e l’analisi di Fourier non è in grado di evidenziarle.

Short-Time Fourier Analysis

Un passo decisivo per tentare di colmare questa carenza, fu fatto da Dennis Gabor (1946) il quale adattò la trasformata di Fourier per analizzare solo una piccola porzione di segnale alla volta, tecnica chiamata “finestramento” del segnale. L’adattamento di Gabor, chiamato “Short-Time Fourier Transform” (STFT), rappresenta un segnale in una funzione bidimensionale del tempo e della frequenza.

La STFT rappresenta una sorta di compromesso tra una rappresentazione del segnale basata sul tempo e sulla frequenza. Essa fornisce informazioni riguardo a “quando” e a “quali frequenze” un evento presente sul segnale analizzato si sia verificato. La precisione con cui è possibile ottenere queste informazioni è comunque limitata e dipende dalle dimensioni della “finestra”.

Mentre il compromesso della STFT tra informazione nel dominio del tempo e della frequenze può risultare utile, lo svantaggio di questa tecnica è che una volta scelta una particolare dimensione della finestra, essa rimane la stessa per tutte le frequenze presenti. Molti segnali per poter essere meglio analizzati, richiedono un approccio più flessibile in cui sia possibile variare le dimensioni della “finestra” allo scopo di determinare più accuratamente sia il tempo che la frequenza.

L’analisi Wavelet

L’analisi wavelet rappresenta il passo logico successivo: una tecnica di finestramento con dimensioni variabili. Le analisi wavelet permettono di usare un intervallo di tempo lungo se vogliamo ricavare dal segnale più informazioni sul suo contenuto di basse frequenze, e piccoli intervalli se vogliamo indagare sulle alte frequenze.

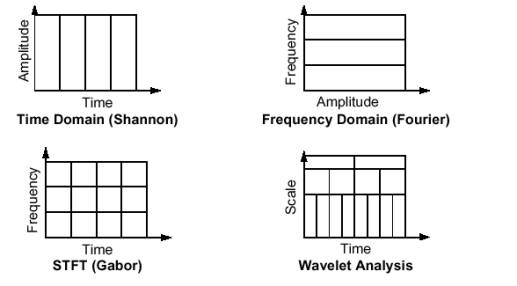
La figura mette a confronto i vari modi di rappresentazione dei segnali basate sul domini del tempo (Shannon), sul dominio delle frequenze (Fourier), STFT e Wavelet.

Notare come l’analisi wavelet non utilizza gli assi tempo-frequenza, ma tempo-scala. Sul concetto di scala si ritornerà in seguito.

Storia delle wavelet

Dal punto di vista storico, l’analisi wavelet è un metodo relativamente nuovo, anche se il suo sviluppo matematico è da far risalire al lavoro di Joseph Fourier nel 19° secolo. Fourier pose le fondamenta con la sua teoria dell’analisi di frequenza, la quale si è dimostrata essere estremamente importante e influente.

L’attenzione dei ricercatori si è andata spostando dalle analisi basate sulla frequenza, alle analisi basate su scala, via via che diventava chiaro che un approccio basato sulla misura media delle fluttuazioni a differenti scale, risultava meno sensibile al rumore.

La parola “wavelet” compare per la prima volta nel 1909, in una tesi di Alfred Haar.

Il concetto di wavelet, nella sua attuale formulazione, è stato proposto per la prima volta da Jean Morlet al Centro di Fisica Teorica di Marsiglia in Francia.

Il metodo dell’analisi wavelet è stato sviluppato soprattutto grazie a Y. Meyer e al suo team che hanno anche contribuito alla sua diffusione. Il principale algoritmo si può far risalire al lavoro di Stephane Mallat nel 1988. Da allora, il metodo è diventato oggetto di studio a livello internazionale e le sue applicazioni coinvolgono moltissimi settori.

Utilità delle wavelet

Uno dei maggiori vantaggi offerti dall’analisi wavelet è di permettere analisi locali ovvero la possibilità di analizzare una singola porzione di un segnale molto lungo.

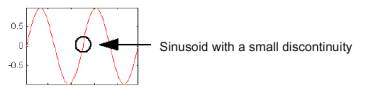
Consideriamo ad esempio un segnale sinusoidale che contenga una piccola discontinuità talmente piccola da non essere facilmente individuabile.

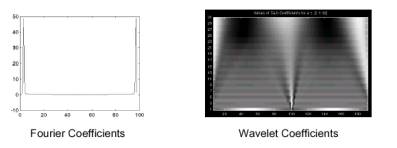
L’analisi di Fourier di un tale segnale non mostrerebbe niente di significativo: uno spettro piatto con i due picchi rappresentanti la singola frequenza.

Viceversa, analizzando lo stesso segnale mediante wavelet, non solo viene messa in evidenza la discontinuità presente nel segnale, ma la stessa viene temporalmente localizzata.

L’analisi wavelet è quindi in grado di rivelare alcuni aspetti del segnale che altre tecniche di analisi non consentono, quali ad esempio trend, punti di discontinuità etc..Inoltre offrendo una visione dei dati diversa da quella consentita dai metodi tradizionali, l’analisi wavelet permette di comprimere o ripulire da rumore qualsiasi segnale, senza alcun apprezzabile decadimento.

Le wavelet, nella loro pur breve storia nel campo dell’analisi dei segnali, hanno già dato prova di essere un ulteriore potente strumento a disposizione degli analisti.

Che cos’è un’analisi wavelet ?

Adesso che conosciamo meglio le possibilità offerte dalle wavelet, la questione successiva riguarda la comprensione di che cosa sia una analisi wavelet ad ancora più fondamentale che cosa sia una wavelet.

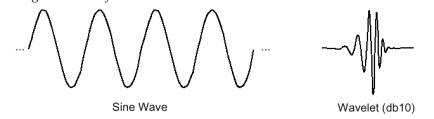
Una wavelet è una forma d’onda di durata limitata e che ha un valore medio uguale a zero.

Confrontando wavelet e sinusoidi (ricordo che queste ultime sono la base dell’analisi di Fourier) emergono chiaramente le seguenti differenze: la sinusoide non ha una durata limitata (essa infatti va da meno infinito a più infinito) è regolare e prevedibile mentre la wavelet è temporalmente finita e tende ad essere irregolare e assimetrica.

L’analisi di Fourier consiste nel decomporre un segnale in sinusoidi di diverse frequenze. Similarmente l’analisi wavelet decompone il segnale in versioni shiftate e scalate della wavelet originale (o onda madre). Osservando la figura si può intuitivamente capire come i segnali che contengono irregolarità possono essere analizzati meglio facendo ricorso ad una wavelet di forma irregolare piuttosto che ad una sinusoide regolare.

La trasformata wavelet continua

Dal punto di vista matematico, l’analisi di Fourier è rappresentata per mezzo della trasformata di Fourier:

F(w) =

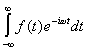
che rappresenta la somma del segnale f(t) moltiplicato per un esponenziale complesso (quest’ultimo può essere scomposto in una componente sinusoidale reale e una complessa) lungo tutto l’intervallo di tempo.

Il risultato della trasformata soni i coefficienti di Fourier F(w) , che moltiplicati per una sinusoide di frequenza w , danno le costituenti sinusoidali del segnale originale. Possiamo rappresentare tale processo in maniera grafica come in figura:

Allo stesso modo, la trasformata wavelet continua (CWT) è definita come la somma, lungo tutto l’intervallo di tempo, del segnale moltiplicato per la versione shiftata e scalata della funzione wavelet Y :

C(scale, position) = Y(scale, position, t) d(t)

Il risultato della CWT sono i coefficienti C , che sono una funzione della scala e della posizione. Moltiplicando ciascun coefficiente per l’appropriata wavelet scalata e shiftata, si ottengono i costituenti wavelet del segnale originale:

Scalamento

Abbiamo già visto che l’analisi wavelet produce un grafico tempo-scala del segnale. Vediamo adesso cosa s’intende per scala e scalamento e per shifting.

Scalare una wavelet significa semplicemente comprimerla: per meglio comprendere ciò introduciamo il fattore di scala indicato con la lettera a .

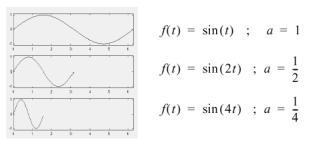
Nel caso di una sinusoide l’effetto del fattore di scala è facilmente visibile:

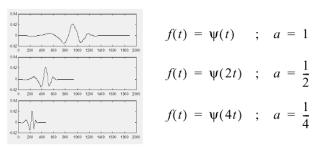
Il fattore di scala agisce esattamente allo stesso modo con le wavelet. Più piccolo è il fattore di scala, più compressa è la wavelet.

Dalle figure risulta chiaro che per una sinusoide sin(wt), il fattore di scala a è correlato inversamente alla frequenza w. Similarmente, nell’analisi wavelet la scala è correlata alla frequenza del segnale. Torneremo successivamente su questo punto.

Shifting

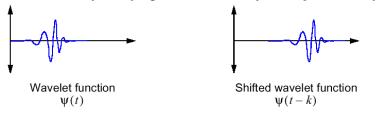
Shiftare una wavelet significa semplicemente spostarla lungo l’asse del tempo (ritardarla o anticiparla). Matematicamente, shiftare una funzione f(t) di k significa avere f(t-k).

Cinque semplici punti per capire meglio la trasformata continua wavelet

Abbiamo definito sopra la trasformata wavelet continua (CWT) come la somma, lungo tutto l’intervallo di tempo, del segnale moltiplicato per la versione shiftata e scalata della funzione wavelet Y . Tale processo crea i coefficienti wavelet che sono una funzione della scala e della posizione. Il processo è realmente semplice. Di seguito esso viene descritto in cinque semplici punti:

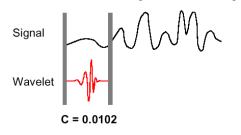
1. scegliere una wavelet e compararla ad una sezione iniziale del segnale originale che vogliamo analizzare.

2. Calcolare un numero C, che rappresenta la correlazione tra la wavelet e la sezione del segnale. Più grande è C, più sono simili wavelet e sezione del segnale. Da notare che il risultato dipenderà dalla forma della wavelet che abbiamo scelto.

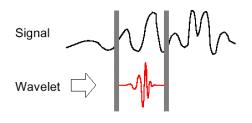
3. Shiftare la wavelet lungo l’asse del tempo e ripetere i punti 1 e 2 fino a coprire l’intero segnale.

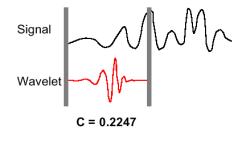
4. Scalare la wavelet e ripetere i passi da 1 a 3.

5. Ripetere i passi da 1 a 4 per tutte le scale.

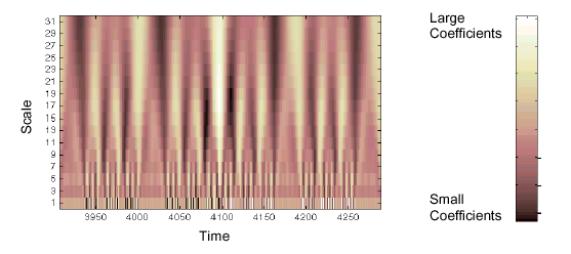
Una volta eseguite le operazioni di cui sopra, si otterranno i coefficienti prodotti a differenti scale, dalle diverse sezioni del segnale. I coefficienti non sono altro che il risultato di una regressione del segnale originale, ottenuta mediante le wavelet. Ma come dare un senso a questi coefficienti? Realizzando un grafico in cui l’asse x rappresenta la posizione lungo il segnale (tempo), l’asse y rappresenta la scala e il colore di ciascun punto di coordinata x,y rappresenta la magnitudo del coefficiente C della wavelet. In figura un grafico generato plottando questi coefficienti.

Questa figura assomiglia molto ad una superficie ondulata vista dall’alto. Se si sposta il punto di osservazione, la stessa immagine avrà questa forma.

I grafici ottenuti mediante la trasformata wavelet continua, sono esattamente una visione tempo-scala del segnale stesso.

Scala e frequenza

Notare nel grafico riportato in precedenza, come la scala va da 1 a 31. Si ricorda che a valori elevati della scala corrispondono wavelet più “allungate” e che più queste ultime sono allungate, più lunga è la porzione di segnale con cui esse vengono comparate.

Esiste quindi una corrispondenza tra la scala delle wavelet e la frequenza :

- Bassi valori di scala => Wavelet compresse => maggiore dettaglio per i cambiamenti rapidi => Alte frequenze w

- Alti valori di scala => Wavelet allungate => dettaglio scarso, caratteristiche principali => basse frequenze w.

E’ importante comprendere che il fatto che l’analisi wavelet non produca una visione tempo- frequenza del segnale non rappresenta un punto debole della tecnica, bensì il suo punto di forza.

Non solo il grafico tempo – scala è un modo differente di vedere i dati, ma esso risulta molto naturale e di facile comprensione.

Consideriamo un panorama lunare, la cui superficie (simulata in figura) sia il risultato di centinaia di bombardamenti di meteoriti le cui dimensioni variano da bolidi giganteschi a particelle di povere.

Se immaginiamo la sezione di questa superficie come un segnale, allora è ragionevole pensare che tale segnale abbia componenti di scala differente, le grandi cavità dovute all’impatto di grandi meteoriti e le piccole caratteristiche dovute all’azione abrasiva di piccoli meteoriti e polveri.

Questo e un tipico caso in cui pensare in termini di scala ha più senso che pensare in termini di frequenza. Osservando il grafico dei coefficienti CWT di tale segnale, emergono caratteristiche particolari che mostrano la possibile natura frattale del segnale. Benchè quello appena visto fosse un segnale artificiale, molti fenomeni naturali, si prestano molto bene ad essere analizzati dalle wavelet.

Bibliografia

Berger A.L., Mèlice J.L. and Van der Mersch I., 1990 “Evolutive spectral analysis of sun spot data over the past 300 Years”, Phil. Trans. R. Soc. London A 330, pag. 529-541.

Birchfield G.E. and Ghil M., 1993, “Climate evolution in the Pliocene-Pleistocene as seen in deep sea records and in simulations: internal variability versus orbital forcing”, J.Geophys. Res. 98 (Do), pag. 10385-10399.

Yiou P., Genthon C., Jouzel J., Ghil M., Le Treut H, Barnola J.M., Lorius C. and Korotkevitch Y.N., 1991, “High-frequency paleovariability in climate and in CO₂levels from Vostok ice-core records”, J. Geophys. Res. 96(B12), pag. 20365-20378.

Grossmann A., Kronland-Martinet R. and Morlet J., 1989, “Reading and understanding continuous wavelet transforms”, in J.M. Combes, A. Grossman and P. Tchamitchian (eds.), Wavelets: Time-Frequency Methods and Phase Space, pp. 2-20, Springer-Verlag, Berlin

Meyer Y., 1989, “Ondelettes et Operateurs I: Ondelettes”, Hermann, Paris.

Mallat S.G., 1989, “A theory for multiresolution signal decomposition: the wavelet representation”, IEEE Trans. Pattern Anal. Mach. Intell. 11(7), pag. 674-693.

Farge M. and Rabreau G., 1988, “Transformèe en ondelettes pour dètecter et analyser les structures coherentes dans les ècoulements turbulents bidimensionels”, C.R. Acad. Sci. Paris 307, pag. 1479-1486.

Gao W. and Li B.L., 1993, “Wavelett analysis of coherent structures at the atmosphere-forest interface”, J. Appl. Meteorol. 32, pag. 1717-1725.

Farge M., 1992, “Wavelet transform and their applications to turbolence”, Ann. Rev. Fluid Mech. 24, pag. 395-457.

Meyers S.D., Kelly B.G. and O’Brien J.J., 1993, “An introduction to wavelet analysis in oceanography and meteorology: with application to the dispersion of Yanai waves”, Mon. Wea. Rev. 121, pag. 2858-2866.

Yiou P., Baert E. and Loutre M.F., 1996, “Spectral analysis of climate data”, Surveys in Geophisics 17, pag. 619-663.